LINK: http://es.wikipedia.org/wiki/Sistema_Internacional_de_Unidades

Sistema Internacional de Unidades

El Sistema Internacional de Unidades, abreviado SI, es el sistema de unidades que se usa en todos los países del mundo, a excepción de tres que no lo han declarado prioritario o único.

Es el heredero del antiguo Sistema Métrico Decimal y por ello también se conoce como «sistema métrico».

Se instauró en 1960, en la XI Conferencia General de Pesas y Medidas, durante la cual inicialmente se reconocieron seis unidades físicas básicas. En 1971 se añadió la séptima unidad básica: el mol.

Una de las características trascendentales, que constituye la gran ventaja del Sistema Internacional, es que sus unidades se basan en fenómenos físicos fundamentales. Excepción única es la unidad de la magnitud masa, el kilogramo, definida como «la masa del prototipo internacional del kilogramo», un cilindro de platinoe iridio almacenado en una caja fuerte de la Oficina Internacional de Pesas y Medidas.^{nota 1}

Las unidades del SI constituyen referencia internacional de las indicaciones de los instrumentos de medición, a las cuales están referidas mediante una concatenación ininterrumpida de calibraciones o comparaciones.

Esto permite lograr equivalencia de las medidas realizadas con instrumentos similares, utilizados y calibrados en lugares distantes y, por ende, asegurar —sin necesidad de duplicación de ensayos y mediciones— el cumplimiento de las características de los productos que son objeto de transacciones en el comercio internacional, su intercambiabilidad.

Entre los años 2006 y 2009 el SI se unificó con la norma ISO 31 para instaurar el Sistema Internacional de Magnitudes (ISO/IEC 80000, con las siglas ISQ).

Unidades básicas (fundamentales)

El Sistema Internacional de Unidades consta de siete unidades básicas (fundamentales), que expresan magnitudes físicas. A partir de estas se determinan el resto de unidades (derivadas):¹

Magnitud física básica	Símbolo dimensional	Unidad básica	Símbolo de la unidad	Definición
Longitud	L	metro	m	Longitud que en el vacío recorre la luz durante un 1/299 792 458 de segundo. De aquí resulta que la velocidad de la luz en el vacío es igual a 299 792 458 metros por segundo exactamente.
Masa	M	kilogramo^{nota 2}	kg	Masa del prototipo internacional del kilogramo, adoptado por la Conferencia General de Pesas y Medidas y depositado en la Oficina Internacional de Pesas y Medidas, en Sèvres, Francia. Este prototipo es un cilindro de 39 mm de altura y 39 mm de diámetro de una aleación 90% de platino y 10% deiridio; tiene una densidad de 21 500 kg/m³.
Tiempo	T	segundo	s	Duración de 9 192 631 770 periodos de la radiación de transición entre los dos niveles hiperfinos del estado fundamental del átomo de cesio 133.
Intensidad de corriente eléctrica	I	amperio	A	Intensidad de una corriente constante que manteniéndose en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y situados a una distancia de un metro uno de otro en el vacío, produciría una fuerza igual a 2·10⁻⁷ newton por metro de longitud.
Temperatura termodinámica	Q	kelvin	K	1/273,16 de la temperatura termodinámica del punto triple del agua. De aquí resulta que la temperatura termodinámica del punto triple del agua es igual a 273,16 kelvin exactamente. El cero de la escala Kelvin coincide con el cero absoluto (−273,15 ºC).²
Cantidad de sustancia	N	mol	mol	Cantidad de sustancia que hay en tantas entidades elementales como átomos hay en 0,012 kg del isótopo carbono-12. Esta definición se refiere a átomos de carbono-12 no ligados, en reposo y en su estado fundamental. Cuando se emplee el mol, es necesario especificar las unidades elementales, que pueden ser átomos, moléculas, iones,electrones u otras partículas o grupos específicos de tales partículas. De aquí resulta que la masa molar del carbono 12 es igual a 12 g por mol, exactamente, M(¹²C) = 12 g/mol.
Intensidad luminosa	J	candela	cd	Intensidad luminosa, en una dirección dada, de una fuente que emite una radiación monocromática de frecuencia 5,4·10¹⁴ Hz y cuya intensidad energética en dicha dirección es 1/683 vatios por estereorradián. De aquí resulta que la eficacia luminosa espectral de una radiación monocromática de frecuencia igual a 5,4·10¹⁴ Hz es igual a 683 lúmenes por vatio.

Las unidades pueden llevar prefijos del Sistema Internacional, que van de 1000 en 1000: múltiplos (ejemplo: kilo indica mil; 1 km = 1000 m), o submúltiplos (ejemplo: mili indica milésima; 1 mA = 0,001 A).

Múltiplos (en mayúsculas a partir de Mega): deca (da), hecto (h), kilo (k), mega (M), giga (G), tera (T), peta (P), exa (E), zetta (Z), yotta (Y).
Submúltiplos (en minúsculas): deci (d), centi (c), mili (m), micro (μ), nano (n), pico (p), femto (f), atto (a), zepto (z), yocto (y).

Unidades derivadas

Mediante esta denominación se hace referencia a las unidades utilizadas para expresar magnitudes físicas que son resultado de combinar magnitudes físicas básicas.

No se debe confundir este concepto con los de múltiplos y submúltiplos, que se utilizan tanto en las unidades básicas como en las derivadas, sino que siempre se le ha de relacionar con las magnitudes expresadas.

Si éstas son longitud, masa, tiempo, intensidad de corriente eléctrica, temperatura, cantidad de substancia o intensidad luminosa, se trata de una magnitud básica. Todas las demás son derivadas.

Ejemplos de unidades derivadas

Unidad de volumen o metro cúbico, resultado de combinar tres veces la longitud.
Unidad de densidad o cantidad de masa por unidad de volumen, resultado de combinar masa (magnitud básica) con volumen (magnitud derivada). Se expresa en kilogramos por metro cúbico. Carece de nombre especial.
Unidad de fuerza, magnitud que se define a partir de la segunda ley de Newton (fuerza = masa × aceleración). La masa es una de las magnitudes básicas; la aceleración es derivada. Por tanto, la unidad resultante (kg • m • s⁻²) es derivada, de nombre especial: newton.^{nota 3}
Unidad de energía. Es la energía necesaria para mover un objeto una distancia de un metro aplicándole una fuerza de un newton; es decir, fuerza por distancia. Se le denomina julio (unidad) (en inglés, joule). Su símbolo es J. Por tanto, J = N • m.

En cualquier caso, mediante las ecuaciones dimensionales correspondientes, siempre es posible relacionar unidades derivadas con básicas.

Definiciones de las unidades derivadas

Unidades con nombre especial

Hertz o hercio (Hz). Unidad de frecuencia.

Definición: un hercio es un ciclo por segundo.

\mathrm{Hz=\frac{1}{s}=s^{-1}}

Newton (N). Unidad de fuerza.

Definición: un newton es la fuerza necesaria para proporcionar una aceleración de 1 m/s² a un objeto cuya masa sea de 1 kg.

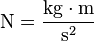
\mathrm{\,N =\frac{kg\cdot m}{s^2}}

Pascal (Pa). Unidad de presión.

Definición: un pascal es la presión normal (perpendicular) que una fuerza de un newton ejerce sobre una superficie de un metro cuadrado.

\mathrm{Pa=\frac{N}{m^2}=\frac{kg}{s^2 \cdot m}}

Julio o Joule (J). Unidad de trabajo y energía.

Definición: un julio es el trabajo realizado por una fuerza de 1 newton para desplazar 1 m en la dirección de la fuerza a un objeto cuya masa sea de 1 kg.

\mathrm{\,J =\frac{kg\cdot m^2}{s^2}}

Vatio (W). Unidad de potencia.

Definición: un vatio es la potencia que genera una energía de un julio por segundo. En términos eléctricos, un vatio es la potencia producida por una diferencia de potencialde un voltio y una corriente eléctrica de un amperio.

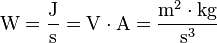
\mathrm{W=\frac{J}{s}=V\cdot A=\frac{m^2\cdot kg}{s^3}}

Culombio (C). Unidad de carga eléctrica.

Definición: un culombio es la cantidad de electricidad que una corriente de un amperio de intensidad transporta durante un segundo.

\mathrm{C=F\cdot V=A\cdot s}

Voltio (V). Unidad de potencial eléctrico y fuerza electromotriz.

Definición: diferencia de potencial a lo largo de un conductor cuando una corriente eléctrica de una intensidad de un amperio utiliza un vatio de potencia.

\mathrm{V=\frac{J}{C}=\frac{m^2\cdot kg}{s^3\cdot A}}

Ohmio (Ω). Unidad de resistencia eléctrica.

Definición: un ohmio es la resistencia eléctrica existente entre dos puntos de un conductor cuando -en ausencia de fuerza electromotriz en éste- una diferencia de potencial constante de un voltio aplicada entre esos dos puntos genera una corriente de intensidad de un amperio.

\Omega=\dfrac{\mbox{V}}{\mbox{A}}=\dfrac{\mbox{m}^2 \cdot \mbox{kg}}{\mbox{s}^{3} \cdot \mbox{A}^2}

Siemens (S). Unidad de conductancia eléctrica.

Definición: un siemens es la conductancia eléctrica existente entre dos puntos de un conductor de un ohmio de resistencia.

\mathrm{S=\frac{1}{\Omega}=\Omega^{-1}}

Faradio (F). Unidad de capacidad eléctrica.

Definición: un faradio es la capacidad de un conductor que con la carga estática de un culombio adquiere una diferencia de potencial de un voltio.

\mbox{F} =\,\mathrm \frac{A \cdot s}{V} =\dfrac{\mbox{C}}{\mbox{V}} =\dfrac{\mbox{C}^2}{\mbox{J}} =\dfrac{\mbox{C}^2}{\mbox{N} \cdot \mbox{m}} =\dfrac{\mbox{s}^2 \cdot \mbox{C}^2}{\mbox{m}^{2} \cdot \mbox{kg}} =\dfrac{\mbox{s}^4 \cdot \mbox{A}^2}{\mbox{m}^{2} \cdot \mbox{kg}}

Tesla (T). Unidad de densidad de flujo magnético e intensidad de campo magnético.

Definición: un tesla es una inducción magnética uniforme que, repartida normalmente sobre una superficie de un metro cuadrado, a través de esta superficie produce un flujo magnético de un weber.

\mathrm{T=\frac{Wb}{m^2}=\frac{V\cdot s}{m^2}=\frac{kg}{C\cdot s}=\frac{kg}{s^2\cdot A}}

Weber (Wb). Unidad de flujo magnético.

Definición: un weber es el flujo magnético que al atravesar un circuito uniespiral genera en éste una fuerza electromotriz de un voltio si se anula dicho flujo en un segundo por decrecimiento uniforme.

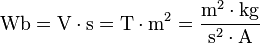
\mathrm{Wb=V\cdot s=T \cdot m^2=\frac{m^2\cdot kg}{s^2\cdot A}}

Henrio (H). Unidad de inductancia.

Definición: un henrio es la inductancia de un circuito en el que una corriente que varía a razón de un amperio por segundo da como resultado una fuerza electromotriz autoinducida de un voltio.

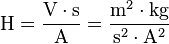
\mathrm{H=\frac{V\cdot s}{A}=\frac{m^2\cdot kg}{s^2\cdot A^2}}

Radián (rad). Unidad de ángulo plano.

Definición: un radián es el ángulo que limita un arco de circunferencia cuya longitud es igual al radio de la circunferencia.

\mathrm{rad=\frac{m}{m}=1}

Estereorradián (sr). Unidad de ángulo sólido.

Definición: un estereorradián es el ángulo sólido que, teniendo su vértice en el centro de una esfera, sobre la superficie de ésta cubre un área igual a la de un cuadrado cuyo lado equivalga al radio de la esfera.

\mathrm{sr=rad^2=\frac{m^2}{m^2}=1}

Lumen (lm). Unidad de flujo luminoso.

Definición: un lumen es el flujo luminoso producido por una candela de intensidad luminosa, repartida uniformemente en un estereorradián.

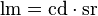
\mathrm{lm=cd\cdot sr}

Lux (lx). Unidad de iluminancia.

Definición: un lux es la iluminancia generada por un lumen de flujo luminoso, en una superficie equivalente a la de un cuadrado de un metro por lado.

\mathrm{lx=\frac{cd\cdot sr}{m^2}}

Becquerelio (Bq). Unidad de actividad radiactiva.

Definición: un becquerel es una desintegración nuclear por segundo.

\mathrm{Bq=\frac{1}{s}=s^{-1}}

Gray (Gy). Unidad de dosis de radiación absorbida.

Definición: un gray es la absorción de un julio de energía ionizante por un kilogramo de material irradiado.

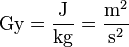
\mathrm{Gy=\frac{J}{kg}=\frac{m^2}{s^2}}

Sievert (Sv). Unidad de dosis de radiación absorbida equivalente.

Definición: un sievert es la absorción de un julio de energía ionizante por un kilogramo de tejido vivo irradiado.

\mathrm{Sv=\frac{J}{kg}=\frac{m^2}{s^2}}

Katal (kat). Unidad de actividad catalítica.

Definición: un katal es la actividad catalítica responsable de la transformación de un mol de compuesto por segundo.

\mathrm{kat=\frac{mol}{s}}

Unidades aceptadas por el SI

El SI ha aceptado como unidades legales una serie de unidades de sistemas anteriores.

Litro (l o L). Unidad de volumen igual a 1 dm³.
Bar o baria (bar). Unidad de presión, equivalente a 100 kPa, un poco menos que la presión atmosférica (que, en condiciones normales, es igual a 101,3 kPa). Se utiliza a menudo su submúltiplo, el milibar.
Grado Celsius (°C). Unidad de temperatura termodinámica.

Definición: la magnitud de un grado Celsius (1 °C) es igual a la de un kelvin.

t/\mathrm{^\circ C}=T/\mathrm{K}-273{,}15

, donde t es la temperatura en grados Celsius, y T en kelvin.

hectárea (ha). Unidad de superficie.

Definición: procede del área, antigua medida de superficie del Sistema Métrico Decimal, igual a 1 dam², luego

1 ha = 100 áreas = 1 hm²

tonelada métrica (T). Unidad de masa, equivalente a 10 kg.

Asimismo se aceptan las medidas de tiempo día, hora y minuto, la medida de longitud milla marina (= 1852 m}, así como la medida de velocidad, nudo, equivalente a una milla marina por hora, (1852 m/h = 1852/3600 m/s).

Unidades derivadas sin nombre especial

En principio, las unidades básicas se pueden combinar libremente para generar otras unidades. A continuación se incluyen las importantes.

Unidad de área.

Definición: un metro cuadrado es el área equivalente a la de un cuadrado de un metro por lado.

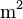
\mathrm{m}^2 \,

Unidad de volumen.

Definición: un metro cúbico es el volumen equivalente al de un cubo de un metro por lado.

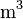
\mathrm{m}^3 \,

Unidad de velocidad o de rapidez.

Definición: un metro por segundo es la velocidad de un cuerpo que, con movimiento uniforme, en un segundo recorre una longitud de un metro.

\frac{\mathrm{m}}{\mathrm{s}}

Unidad de ímpetu lineal o cantidad de movimiento.

Definición: es la cantidad de movimiento de un cuerpo con una masa de un kilogramo que se mueve a una velocidad instantánea de un metro por segundo.

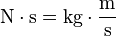
\mathrm{N\cdot s}=\mathrm{kg}\cdot\frac{\mathrm{m}}{\mathrm{s}}

Unidad de aceleración.

Definición: es el aumento de velocidad regular -que afecta a un objeto- equivalente a un metro por segundo cada segundo.

\frac{\mathrm{m}}{\mathrm{s}^2}

Unidad de número de onda.

Definición: es el número de onda de una radiación monocromática cuya longitud de onda es igual a un metro.

\frac{1}{\mathrm{m}}

Unidad de velocidad angular.

Definición: es la velocidad de un cuerpo que, con una rotación uniforme alrededor de un eje fijo, en un segundo gira un radián.

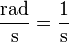
\frac{\mathrm{rad}}{\mathrm{s}}=\frac{1}{\mathrm{s}}

Unidad de aceleración angular.

Definición: es la aceleración angular de un cuerpo sujeto a una rotación uniformemente variada alrededor de un eje fijo, cuya velocidad angular, en un segundo, varía un radián.

\frac{\mathrm{rad}}{\mathrm{s}^2}=\frac{1}{\mathrm{s}^2}

Unidad de momento de fuerza y torque.

Definición: es el momento o torque generado cuando una fuerza de un newton actúa a un metro de distancia del eje fijo de un objeto e impulsa la rotación de éste.

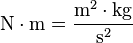
\mathrm{N\cdot m}=\frac{\mathrm{m^2\cdot kg}}{\mathrm{s}^2}

Unidad de viscosidad dinámica.

Definición: es la viscosidad dinámica de un fluido homogéneo, en el cual, cuando hay una diferencia de velocidad de un metro por segundo entre dos planos paralelos separados un metro, el movimiento rectilíneo y uniforme de una superficie plana de un metro cuadrado provoca una fuerza retardatriz de un newton.

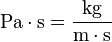
\mathrm{Pa\cdot s}=\frac{\mathrm{kg}}{\mathrm{m\cdot s}}

Unidad de entropía.

Definición: es el aumento de entropía de un sistema que -siempre que en el sistema no ocurra transformación irreversible alguna- a la temperatura termodinámica constante de un kelvin recibe una cantidad de calor de un julio.

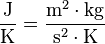
\mathrm{\frac{J}{K}}=\mathrm{\frac{m^2\cdot kg}{s^2\cdot K}}

Unidad de calor específico o capacidad calorífica.

Definición: es la cantidad de calor, expresada en julios, que, en un cuerpo homogéneo de una masa de un kilogramo, produce una elevación de temperatura termodinámicade un kelvin.

\mathrm{\frac{J}{kg\cdot K}}=\mathrm{\frac{m^2}{s^2\cdot K}}

Unidad de conductividad térmica.

Definición: es la conductividad térmica de un cuerpo homogéneo isótropo en la que una diferencia de temperatura de un kelvin entre dos planos paralelos de un metro cuadrado y distantes un metro, entre estos planos genera un flujo térmico de un vatio.

\mathrm{\frac{W}{m\cdot K}}=\mathrm{\frac{m\cdot kg}{s^3\cdot K}}

Unidad de intensidad del campo eléctrico.

Definición: es la intensidad de un campo eléctrico que ejerce una fuerza de un newton sobre un cuerpo cargado con una cantidad de electricidad de un culombio.

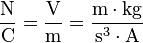
\mathrm{\frac{N}{C}}=\mathrm{\frac{V}{m}}=\mathrm{\frac{m\cdot kg}{s^3\cdot A}}

Unidad de rendimiento luminoso.

Definición: es el rendimiento luminoso obtenido de un artefacto que gasta un vatio de potencia y genera un lumen de flujo luminoso.

\mathrm{\frac{lm}{W}}=\mathrm{\frac{cd\cdot sr\cdot s^3}{m^2\cdot kg}}=\mathrm{\frac{cd\cdot s^3}{m^2\cdot kg}}

Normas ortográficas relativas a los símbolos

Los símbolos de las unidades son entes matemáticos, no abreviaturas. Por ello deben escribirse siempre tal cual están establecidos (ejemplos: «m» para metro y «A» para amperio), precedidos por el correspondiente valor numérico, en singular, ya que como tales símbolos no forman plural.

Al expresar las magnitudes numéricamente, se deben usar los símbolos de las unidades, nunca los nombres de unidades. Por ejemplo: «50 kHz», nunca «50 kilohercios»; aunque sí podríamos escribir «cincuenta kilohercios», pero no «cincuenta kHz».

El valor numérico y el símbolo de las unidades deben ir separados por un espacio, y no deben quedar en líneas diferentes (espacio duro). Ejemplo: 50 m es correcto, mientras que 50m es incorrecto).⁴ ⁵

Los símbolos de las unidades SI se expresan con minúsculas. Si dichos símbolos corresponden a unidades derivadas de nombres propios (apellidos), su letra inicial es mayúscula (W de Watt, V de Volta, Wb de Weber, Ω —omega mayúscula— de Ohm, etcétera).

Para evitar confusiones con el número 1 se puede exceptuar el litro, cuyo símbolo puede escribirse también como L mayúscula.⁶ El uso de una letra ele minúscula ovoide en la parte superior y abierta en la porción inferior; así: ·"ℓ", no está reconocido por el CIPM.⁷ En cualquier caso, el Comité Internacional de Pesos y Medidas recomienda que los resultados de mediciones precisas de volumen se expresen en unidades del Sistema Internacional y no en litros.

Asímismo, los submúltiplos y los múltiplos, incluido el kilo (k), se escriben con minúscula. Desde mega hacia valores superiores se escriben con mayúscula. Se han de escribir enletra redonda (no en bastardillas), independientemente del resto del texto.⁸ ⁹ Por ejemplo: mide 20 km de longitud. Esto permite diferenciarlos de las variables.

Los símbolos no se pluralizan, no cambian aunque su valor no sea la unidad, es decir, no se debe añadir una s. Tampoco ha de escribirse punto (.) a continuación de un símbolo, a menos que sea el que sintácticamente corresponde al final de una frase.

Por lo tanto es incorrecto escribir, por ejemplo, el símbolo de kilogramos como Kg (con mayúscula), kgs (pluralizado) o kg. (con punto). El único modo correcto de simbolizarlo es «kg».

La razón es que se procura evitar malas interpretaciones: «Kg», podría entenderse como kelvin • gramo, ya que «K» es el símbolo de la unidad de temperatura kelvin. A propósito de esta unidad, se escribe sin el símbolo de grados «°», pues su nombre correcto no es «grado Kelvin» °K, sino sólo kelvin (K).⁹

El símbolo de segundos es «s» (en minúscula, sin punto posterior), no seg, ni segs. Los amperios no se han de abreviar Amps., ya que su símbolo es A (con mayúscula, sin punto). Metro se simboliza con m (no Mt, ni M, ni mts.).

Normas ortográficas referentes a los nombres

Al contrario que los símbolos, los nombres relativos a aquellos no están normalizados internacionalmente, sino que dependen de la lengua nacional donde se usen (así lo establece explícitamente la norma ISO 80000). Según el SI, se consideran siempre sustantivos comunes y se tratan como tales (se escriben con minúsculas).

Las designaciones de las unidades instituidas en honor de científicos eminentes mediante sus apellidos deben escribirse con ortografía idéntica a tales apelativos, pero con minúscula inicial. No obstante son igualmente aceptables sus denominaciones castellanizadas de uso habitual, siempre que hayan sido reconocidas por la Real Academia Española. Ejemplos: amperio, culombio, faradio, voltio, vatio, etcétera.

Normas referentes a los números

El separador decimal debe estar alineado con los dígitos, mediante una coma (,), salvo en textos en inglés, en los cuales se emplea punto (.). No se ha de usar otro signo entre los números.

Para facilitar la lectura, los guarismos pueden agruparse en grupos de tres, de derecha a izquierda, sin utilizar comas, ni puntos, en los espacios entre grupos. El número completo debe quedar en la misma línea (espacio duro). Ejemplo: 123 456 789 987 546.

Para este efecto, en algunos países se acostumbra separar los miles con un punto (ejemplo: 123.456.789.987.546). Esta notación es desaconsejable y ajena a la normativa establecida en el Sistema Internacional de Unidades.¹⁰

En escritos referentes a fechas se exceptúan las cifras relativas a años: 2012 en vez de 2 012.

Tabla de múltiplos y submúltiplos

1000ⁿ	10ⁿ	Prefijo	Símbolo	Escala corta	Escala larga	Equivalencia decimal en los Prefijos del Sistema Internacional	Asignación
1000⁸	10²⁴	yotta	Y	Septillón	Cuatrillón	1 000 000 000 000 000 000 000 000	1991
1000⁷	10²¹	zetta	Z	Sextillón	Mil trillones	1 000 000 000 000 000 000 000	1991
1000⁶	10¹⁸	exa	E	Quintillón	Trillón	1 000 000 000 000 000 000	1975
1000⁵	10¹⁵	peta	P	Cuatrillón	Mil billones	1 000 000 000 000 000	1975
1000⁴	10¹²	tera	T	Trillón	Billón	1 000 000 000 000	1960
1000³	10⁹	giga	G	Billón	Mil millones / Millardo	1 000 000 000	1960
1000²	10⁶	mega	M	Millón		1 000 000	1960
1000¹	10³	kilo	k	Mil / Millar		1 000	1795
1000^2/3	10²	hecto	h	Cien / Centena		100	1795
1000^1/3	10¹	deca	da	Diez / Decena		10	1795
1000⁰	10⁰	ninguno		Uno / Unidad		1
1000^−1/3	10⁻¹	deci	d	Décimo		0,1	1795
1000^−2/3	10⁻²	centi	c	Centésimo		0,01	1795
1000⁻¹	10⁻³	mili	m	Milésimo		0,001	1795
1000⁻²	10⁻⁶	micro	µ	Millonésimo		0,000 001	1960
1000⁻³	10⁻⁹	nano	n	Billonésimo	Milmillonésimo	0,000 000 001	1960
1000⁻⁴	10⁻¹²	pico	p	Trillonésimo	Billonésimo	0,000 000 000 001	1960
1000⁻⁵	10⁻¹⁵	femto	f	Cuatrillonésimo	Milbillonésimo	0,000 000 000 000 001	1964
1000⁻⁶	10⁻¹⁸	atto	a	Quintillonésimo	Trillonésimo	0,000 000 000 000 000 001	1964
1000⁻⁷	10⁻²¹	zepto	z	Sextillonésimo	Miltrillonésimo	0,000 000 000 000 000 000 001	1991
1000⁻⁸	10⁻²⁴	yocto	y	Septillonésimo	Cuatrillonésimo	0,000 000 000 000 000 000 000 001	1991

Legislación acerca del uso del SI

El SI se puede usar legalmente en cualquier país, incluso donde aún no lo hayan implantado. En muchas otras naciones su uso es obligatorio. A efectos de conversión de unidades, en los países que todavía utilizan otros sistemas de unidades de medidas, como los Estados Unidos y el Reino Unido, se acostumbra indicar las unidades del SI junto a las propias.

El Sistema Internacional se adoptó a partir de la undécima Conferencia General de Pesas y Medidas (CGPM o Conférence Générale des Poids et Mesures), en 1960.

En Argentina el SI se adoptó en virtud de la ley N.º 19.511, sancionada el 2 de marzo de 1972, conocida como Sistema Métrico Legal Argentino (SIMELA).
En Chile se adoptó el Sistema Métrico Decimal el 29 de enero de 1848 según la Ley de Pesos y Medidas.
En Colombia se adoptó mediante el Decreto de la República N.º 2416 el 9 de diciembre de 1971. Por ese medio el gobierno nacional instituyó al ICONTEC como el ente nacional encargado de su regulación y verificación, junto a las gobernaciones y alcaldías de los departamentos, como sus rectores.
En Ecuador se adoptó mediante la Ley N.º 1.456 de Pesas y Medidas, promulgada en el Registro Oficial N.º 468 del 9 de enero de 1974.
En España, el Real Decreto de 14 de febrero de 1879 estableció la obligatoriedad del Sistema Métrico a partir de julio de 1880. El Sistema Internacional fue implantado por la Ley 3/85 Jefatura del Estado; B.O.E. 18/marzo/1985 Declaración del Sistema Internacional de Unidades de Medida (S.I.) como sistema legal. La última actualización de la normativa a este respecto se publicó en 2009, mediante el Real Decreto 2032/2009.¹⁴
En México la inclusión se ejecutó cuando se unió al Tratado del Metro (en su antigua denominación como Sistema Métrico Decimal), en tiempos del presidente Porfirio Díaz, el 30 de diciembre de 1890. Actualmente su definición y su legalización como sistema estándar, legal y oficial están inscritas en la Secretaría de Economía, bajo la modalidad de Norma Oficial Mexicana.¹⁵
En el Perú el Sistema Legal de Unidades de Medida del Perú (SLUMP) entró en vigencia –por la Ley 23560, del 31 de diciembre de 1982– a partir del 31 de marzo de 1983.
En Uruguay entró en vigor el uso obligatorio del SI a partir del 1 de enero de 1983, por medio de la ley 15.298.
En Venezuela, el año 1960, el gobierno nacional aprobó, en todas sus partes, la Convención Internacional relativa al Sistema Métrico y el Reglamento anexo a la referida convención ratificada el 12 de junio de 1876. En el año 1981, mediante una resolución publicada en la Gaceta Oficial Extraordinaria N.º 2.823, de fecha 14 de julio, se dispusieron la especificación y la referencia de las Unidades de Medidas del Sistema Legal Venezolano.

SISTEMA INTERNACIONAL DE UNIDADES

martes, 5 de mayo de 2015